\[ 標準形 \ : \ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \quad (a > 0, \ b > 0) \] \[ a > b > 0のとき、焦点F = (\sqrt{a^2 - b^2}, 0), \ (-\sqrt{a^2 - b^2}, 0) \ で横長の楕円となる。 \] \[ b > a > 0のとき、焦点F = (0, \sqrt{b^2 - a^2}), \ (0, -\sqrt{b^2 - a^2}) \ で縦長の楕円となる。 \]

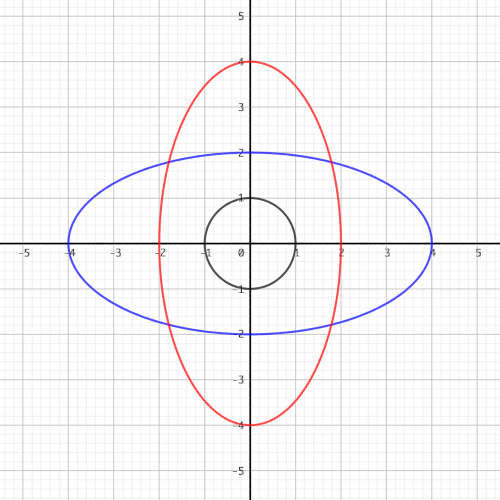
\[ 青 : \frac{x^2}{4^2} + \frac{y^2}{2^2} = 1 \ (a \gt b), \ \ F = (2 \sqrt{3}, 0), (-2 \sqrt{3}, 0) \\ 赤 : \frac{x^2}{2^2} + \frac{y^2}{4^2} = 1 \ (a \lt b), \ \ F = (0, 2 \sqrt{3}), (0, -2 \sqrt{3}) \\ 黒 : \frac{x^2}{1^2} + \frac{y^2}{1^2} = 1 \ (a = b), \ \ F = (0, 0) \]

\[ \frac{(x - p)^2}{a^2} + \frac{(y - q)^2}{b^2} = 1 \ は標準形をx方向にp, \ y方向にqだけずらした楕円となる。 \]

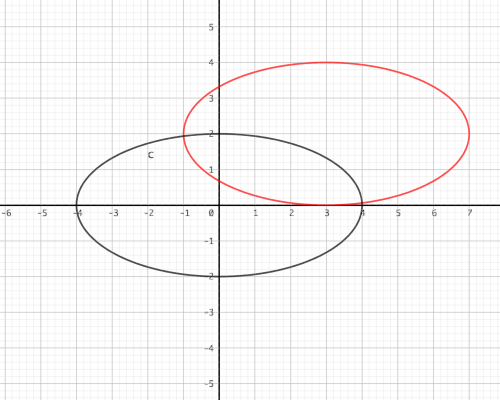
\[ 赤 : \frac{(x-3)^2}{4^2} + \frac{(y-2)^2}{2^2} = 1 \ (a \lt b), \ \ F = (2 \sqrt{3} + 3, 2), (-2 \sqrt{3} + 3, 2) \\ 黒 : \frac{x^2}{4^2} + \frac{y^2}{2^2} = 1 \ F = (0, 0) \\ \]

\[ 楕円\frac{x^2}{a^2} + \frac{y^2}{b^2}=1 \ 上の点(x_0, y_0)における接戦の方程式 \ : \ \frac{x_0 x}{a^2} + \frac{y_0 y}{b^2}=1 \]

\[ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \ (左右), \ 漸近線 \ y = \pm \frac{b}{a}x, \ 焦点 \ F = ( \pm \sqrt{a^2 + b^2}, 0 ), \ 頂点 \ ( \pm a, 0 ) \] \[ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 \ (上下), \ 漸近線 \ y = \pm \frac{b}{a}x, \ 焦点 \ F = ( 0, \pm \sqrt{a^2 + b^2} ), \ 頂点 \ ( 0, \pm b ) \]

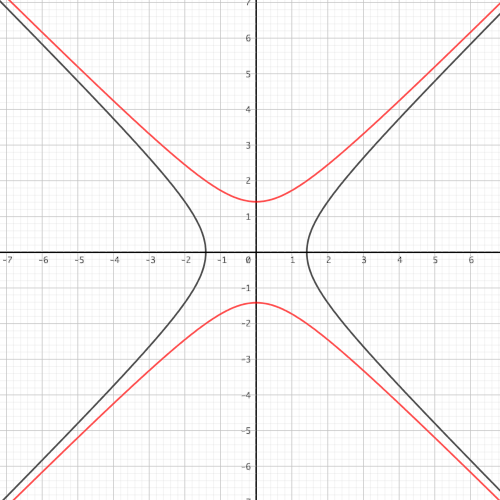
\[ 黒 : \frac{x^2}{2^2} + \frac{y^2}{2^2} = 1 \ (左右) \\ 赤 : \frac{x^2}{2^2} + \frac{y^2}{2^2} = -1 \ (上下) \]

\[ 双曲線\frac{x^2}{a^2} - \frac{y^2}{b^2}= \pm 1 \ 上の点(x_0, y_0)における接戦の方程式 \ : \ \frac{x_0 x}{a^2} - \frac{y_0 y}{b^2} \pm 1 \]

放物線

parabola
\[ y^2=4px : 焦点 \ (p, 0), \ 準線 \ x = -p, \ 接線の方程式 \ yy_1 = 2p(x + x_1) \] \[ x^2=4py : 焦点 \ (0, p), \ 準線 \ y = -p, \ 接線の方程式 \ xx_1 = 2p(y + y_1) \] \[ 焦点を \ F(x_f, y_f) , 放物線上の動点 \ P(x_p, y_p) \ から準線 \ x=x_d への垂線を \ PH \ とすると、常に \ PF=PH \ であり, \sqrt{(x_p-x_f)^2 + (y_p-y_f)^2} = |x - x_d| \ が成り立つ。 \]

\[ 放物線 y^2=4pxの(x_1, y_1)における接戦の方程式 \ : \ y_1 y = 2p(x + x_1) \]