三角関数
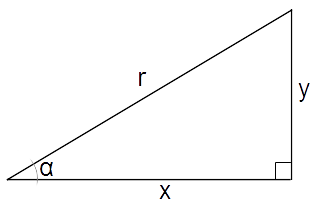
定義
$$ \sin \alpha = \frac {r} {y} $$ $$ \cos \alpha = \frac {r} {x} $$ $$ \tan \alpha = \frac {y} {x} \ \tan \alpha の値は直線の傾きに等しい。 $$
$$ \sin \alpha = \frac {r} {y} $$ $$ \cos \alpha = \frac {r} {x} $$ $$ \tan \alpha = \frac {y} {x} \ \tan \alpha の値は直線の傾きに等しい。 $$
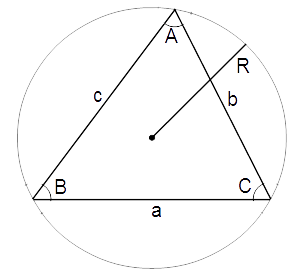
正弦定理
$$ \frac{a}{{\sin}A} = \frac{b}{{\sin}B} = \frac{c}{{\sin}C} = 2R $$
余弦定理
$$ a^2 = b^2 + c^2 - 2bc\cdot{\cos}A $$ $$ b^2 = a^2 + c^2 - 2ac\cdot{\cos}B $$ $$ c^2 = a^2 + b^2 - 2ab\cdot{\cos}C $$
$$ \frac{a}{{\sin}A} = \frac{b}{{\sin}B} = \frac{c}{{\sin}C} = 2R $$
余弦定理
$$ a^2 = b^2 + c^2 - 2bc\cdot{\cos}A $$ $$ b^2 = a^2 + c^2 - 2ac\cdot{\cos}B $$ $$ c^2 = a^2 + b^2 - 2ab\cdot{\cos}C $$
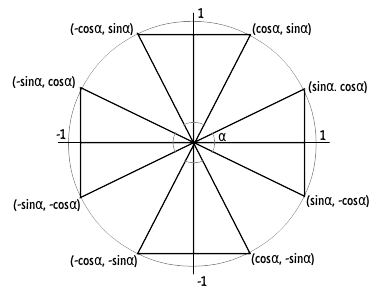
負角公式
$$ {\sin}(-\alpha) = -{\sin}\alpha $$ $$ {\cos}(-\alpha) = {\cos}\alpha $$ $$ {\tan}(-\alpha) = -{\tan}\alpha $$
補角公式 補角:足すと平角になる二つの角
$$ \sin({\pi-\alpha}) = \sin\alpha $$ $$ \cos({\pi-\alpha}) = -\cos\alpha $$ $$ \tan({\pi-\alpha}) = -\tan\alpha $$
余角公式
$$ \sin( \frac{\pi}{2} - \alpha) = \cos\alpha $$ $$ \cos( \frac{\pi}{2} - \alpha) = \sin\alpha $$
$$ {\sin}(-\alpha) = -{\sin}\alpha $$ $$ {\cos}(-\alpha) = {\cos}\alpha $$ $$ {\tan}(-\alpha) = -{\tan}\alpha $$
補角公式 補角:足すと平角になる二つの角
$$ \sin({\pi-\alpha}) = \sin\alpha $$ $$ \cos({\pi-\alpha}) = -\cos\alpha $$ $$ \tan({\pi-\alpha}) = -\tan\alpha $$
余角公式
$$ \sin( \frac{\pi}{2} - \alpha) = \cos\alpha $$ $$ \cos( \frac{\pi}{2} - \alpha) = \sin\alpha $$
加法公式
$$ \sin( \alpha + \beta ) = \sin\alpha\cos\beta + \cos\alpha\sin\beta $$ $$ \sin( \alpha - \beta ) = \sin\alpha\cos\beta - \cos\alpha\sin\beta $$ $$ \cos( \alpha + \beta ) = \cos\alpha\cos\beta - \sin\alpha\sin\beta $$ $$ \cos( \alpha - \beta ) = \cos\alpha\cos\beta + \sin\alpha\sin\beta $$ $$ \tan( \alpha + \beta ) = \frac {\tan\alpha + \tan\beta} {1 - \tan\alpha\tan\beta} $$ $$ \tan( \alpha - \beta ) = \frac {\tan\alpha - \tan\beta} {1 + \tan\alpha\tan\beta} $$
倍角公式
$$ \sin 2 \alpha = 2 \sin \alpha \cos \alpha $$ $$ \cos 2 \alpha = \cos^2 \alpha - \sin^2 \alpha = 2 \cos^2 \alpha - 1 = 1 - 2 \sin^2 \alpha $$ $$ \tan 2 \alpha = \frac {2 \tan \alpha} {1 - \tan^2 \alpha} $$
半角公式
$$ \sin^2 \alpha = \frac {1 - \cos 2 \alpha}{2} $$ $$ \cos^2 \alpha = \frac {1 + \cos 2 \alpha}{2} $$
積和公式
$$ \sin\alpha\cos\beta = \frac{1}{2} ( \sin(\alpha + \beta) + \sin(\alpha - \beta) ) $$ $$ \sin\alpha\sin\beta = - \frac{1}{2} ( \cos(\alpha + \beta) - \cos(\alpha - \beta) ) $$ $$ \cos\alpha\cos\beta = \frac{1}{2} ( \cos(\alpha + \beta) + \cos(\alpha - \beta) ) $$
和積公式
$$ \sin\alpha + \sin\beta = 2\sin \frac{\alpha + \beta}{2} \cos \frac{\alpha - \beta}{2} $$ $$ \sin\alpha - \sin\beta = 2\cos \frac{\alpha + \beta}{2} \sin \frac{\alpha - \beta}{2} $$ $$ \cos\alpha + \cos\beta = 2\cos \frac{\alpha + \beta}{2} \cos \frac{\alpha - \beta}{2} $$ $$ \cos\alpha - \cos\beta = -2\sin \frac{\alpha + \beta}{2} \sin \frac{\alpha - \beta}{2} $$ $$ 和積公式は加法公式から直接ではなく、積和公式に A = \alpha + \beta, B = \alpha - \beta を入力して導き出す。 $$