絶対値 absolute value
$$ | \vec{a} | = \sqrt{a_x^2 + b_y^2 + z_c^2} $$ $$ \vec{a} \cdot \vec{a} = x^2 + y^2 = | \vec{a} |^2 \Longrightarrow \sqrt{ \vec{a} \cdot \vec{a} } = | \vec{a} | $$

内分点 dividing point
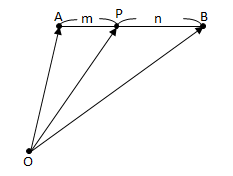$$ 線分 \ AB \ を \ m:n \ に内分する点を \ P \ とすると, \ \vec{p} = \frac{ n \vec{a} + m \vec{b} } { m + n } $$

外分点 externally dividing point
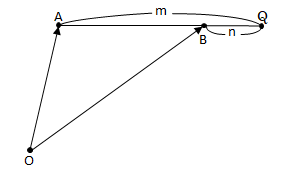$$ 線分 \ AB \ を \ m:n \ に外分する点を \ Q \ とすると, \ \vec{q} = \frac{ -n \vec{a} + m \vec{b} } { m - n } $$

ベクトルの領域
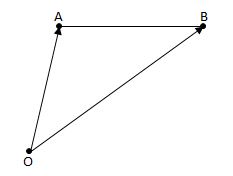$$ 0 \leq s + t \leq 1 \ のとき、 \ s\vec{a} + t\vec{b} = \vec{p} \ は \triangle OABの中に存在する。 \\ s + t = 1 \ のときは、s\vec{a} + t\vec{b} = \vec{p} \ は 直線ABの上に存在する。 $$

内積 inner product
$$ \vec{a} \cdot \vec{b} = (a_x \times b_x + a_y \times b_y + a_z \times b_z) = | \vec{a} | | \vec{b} | \cos \theta $$ $$ \vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a} $$ $$ ( \vec{a} + \vec{b} ) \cdot ( \vec{a} + \vec{b} ) = |a|^2 + \vec{a} \cdot \vec{b} + |b|^2 $$ ベクトルの内積の値はスカラ

外積 cross product
$$ \vec{a} \times \vec{b} = \left( \begin{array}{c} a_y b_z - a_z b_y \\ a_z b_x - a_x b_z \\ a_x b_y - a_y b_x \end{array} \right) $$ $$ | \vec{a} \times \vec{b} | = | \vec{a} | | \vec{b} | \sin \theta $$ ベクトルの外積の値はベクトル

三角形の面積
$$ \triangle OAB \ の面積 \ S = \frac{1}{2} \sqrt{ |\vec{a}|^2 |\vec{b}|^2 - (\vec{a} \cdot \vec{b})^2 } = \frac{1}{2} | a_x b_y - a_b b_x | $$